Photo 1 (486)
[The below text is based on the old numbering of photos presented on the old list of EXIF times.]
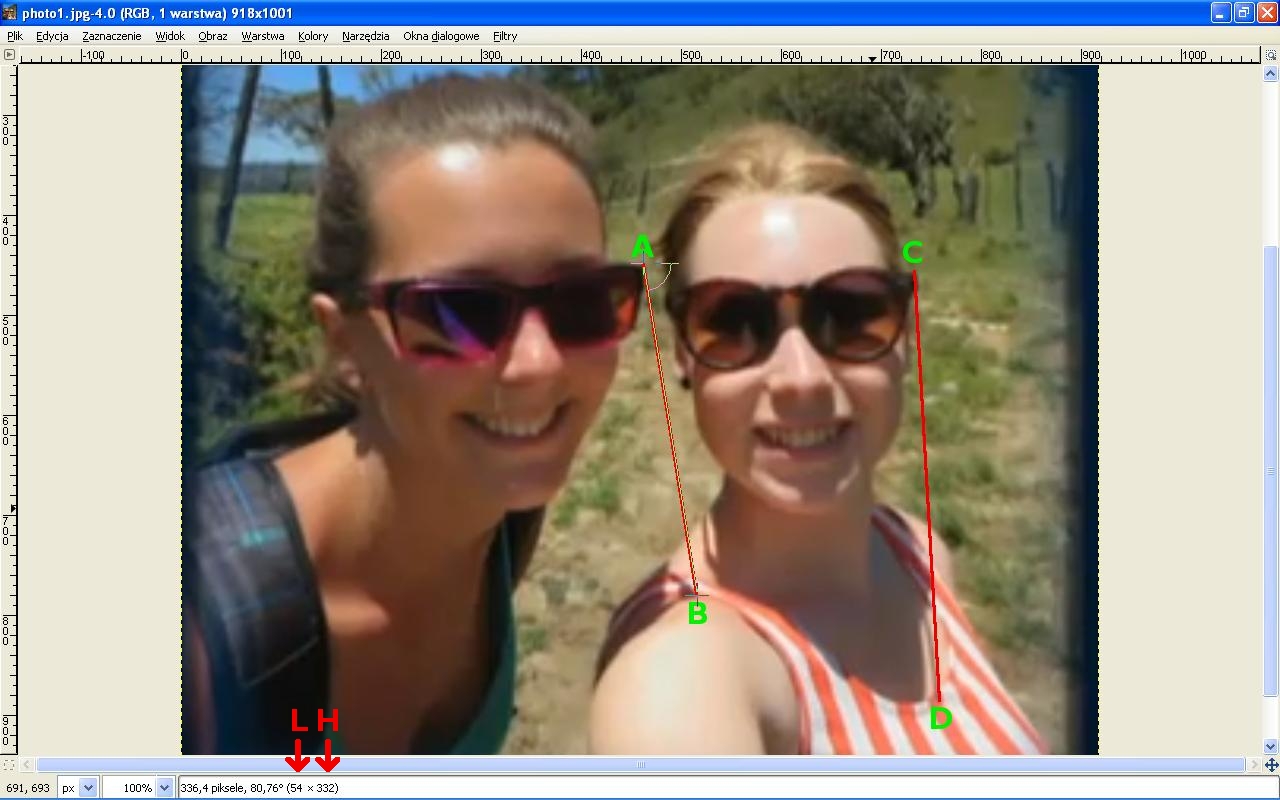
A selfie of Kris and Lisanne taken on the El Pianista trail.
Photo 1
The segments AB and CD were used to determine the time of taking photo 1. I used the Measure Tool in GIMP to measure the height of the object and the length of the cast shadow. In this case the object is abstract: a segment in photo 1.
Photo 1-1
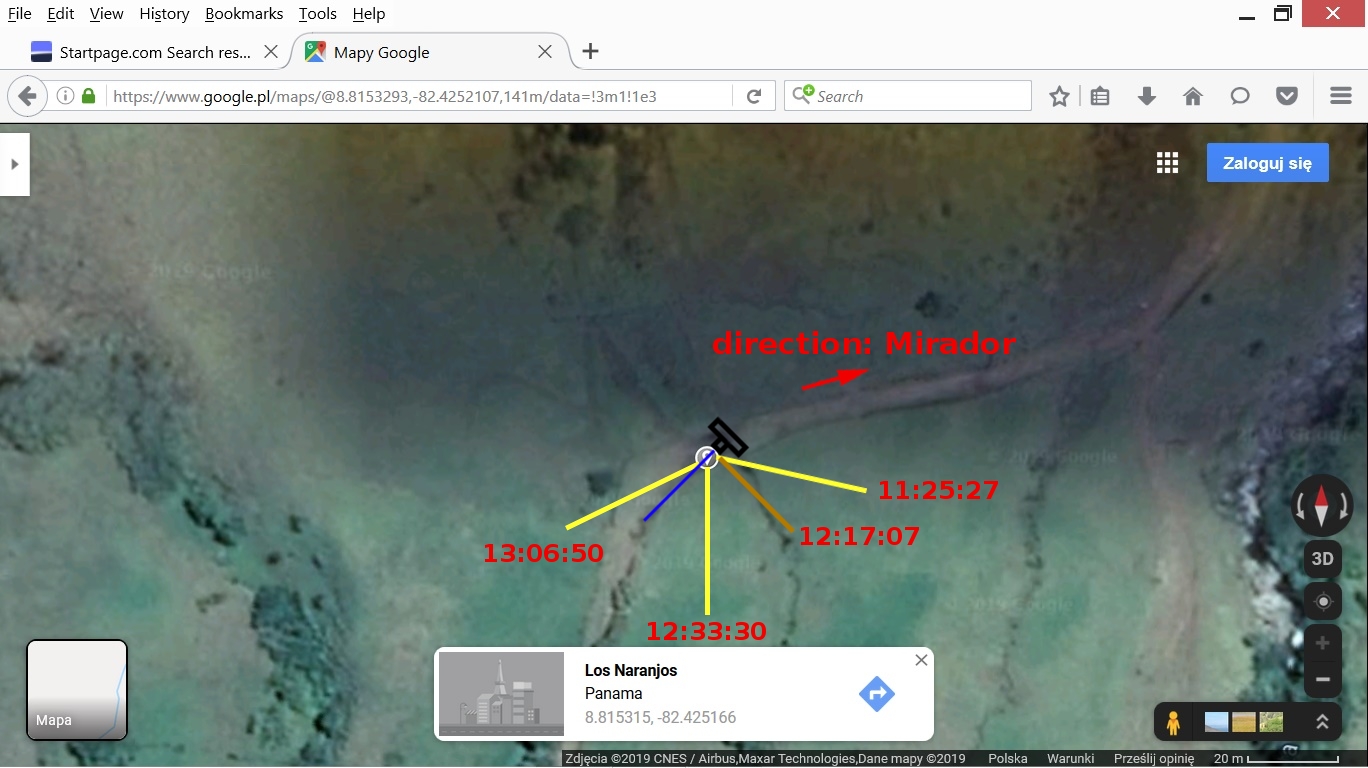
The arrows at the bottom on the left point at the measured values.
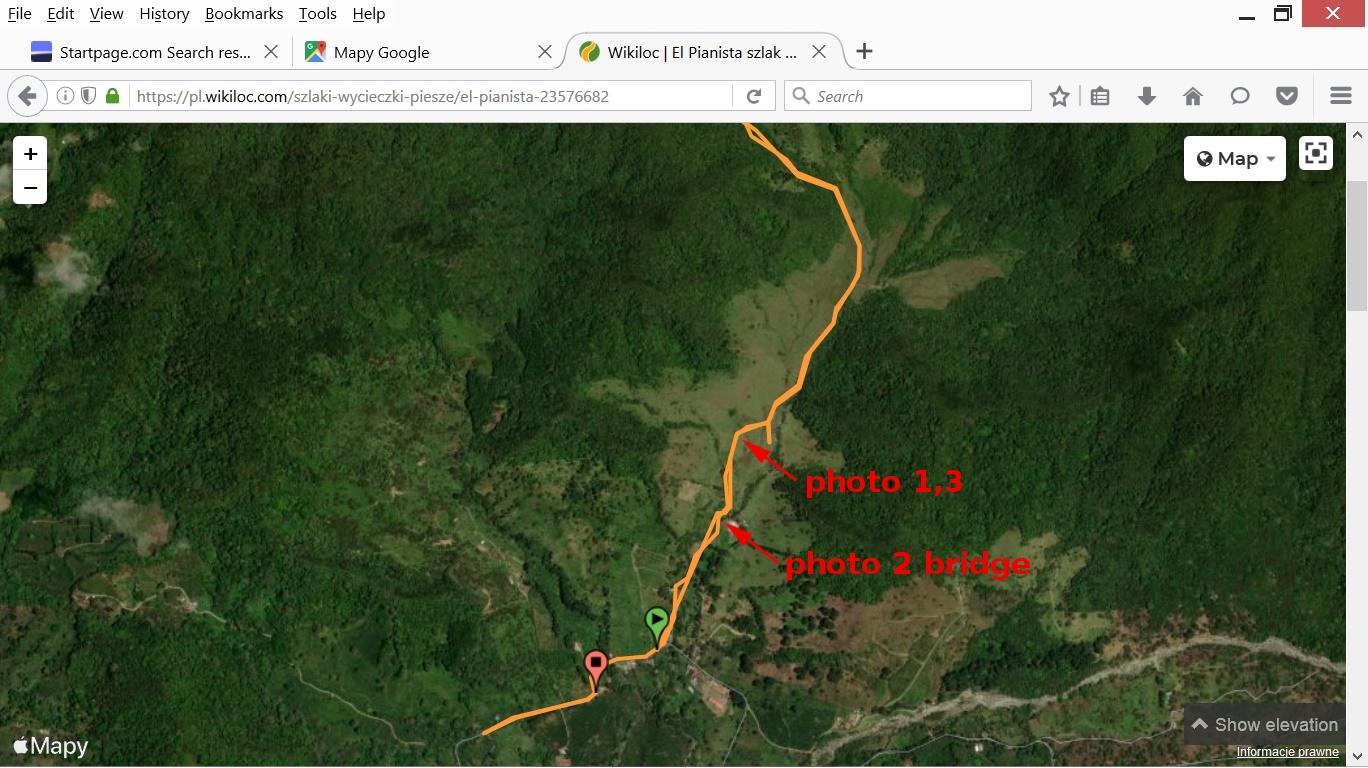
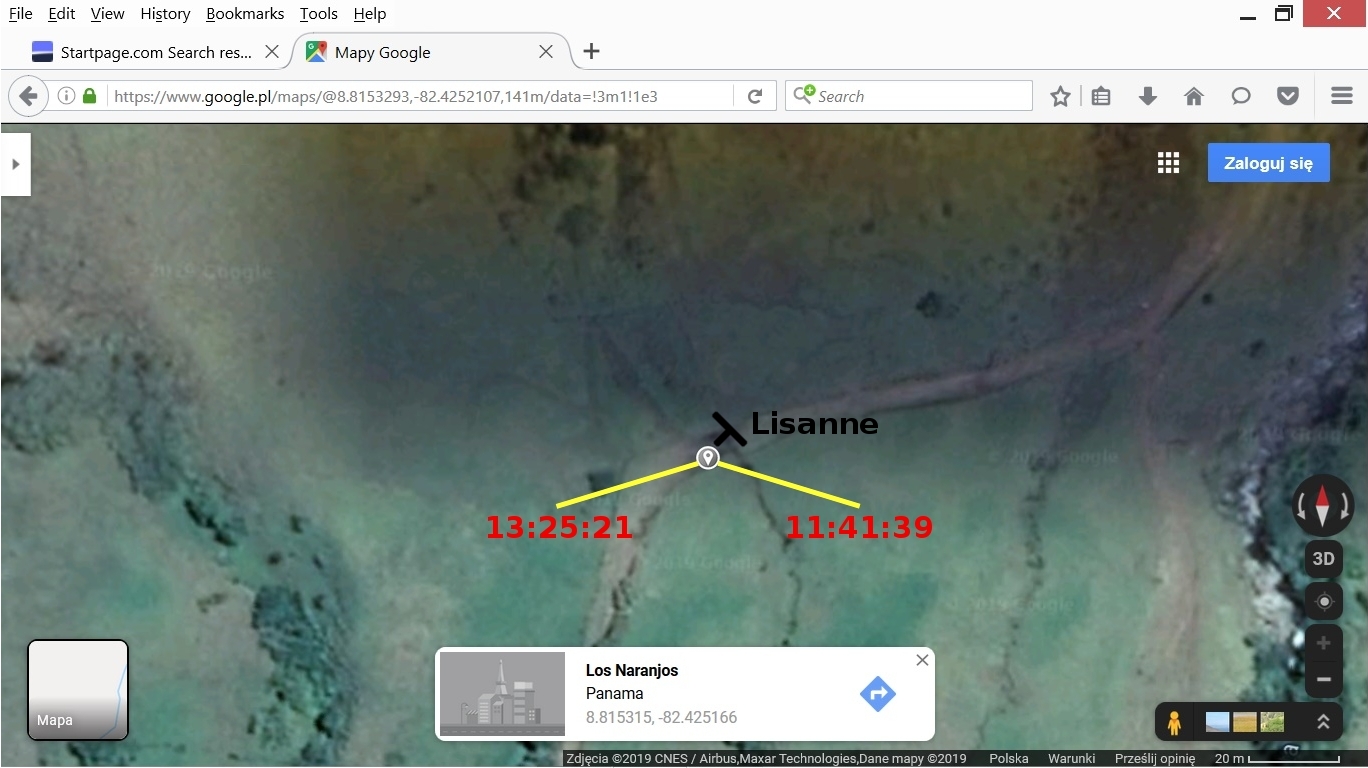
I assumed that the place where photo 1 was taken is the same place where photo 3 was taken. See photos below that justify my assumption (photos from 1-8 to 1-12). See my analysis of photo 3 to check how I determined the coordinates (latitude and longitude) for calculations.
This is a map of the El Pianista trail with marked places where photos 1, 2, 3 were taken.
Photo 1-2
We have the following data needed to calculate the time of taking photo 1:
Segment AB:
L = 54.0 pixels
H = 332.0 pixels
date = 2014-04-01 (April 1st 2014)
latitude = 8.815315
longitude = -82.425166
time zone = -5
DST = 0 (Daylight Saving Time, there is no DST in Panama)
The results obtained by means of method 1 (here is a description of method 1):
elevation = 80.76 deg. (cell B55 in the spreadsheet)
local time 1 = 13:06:50
azimuth 1 = 244.09 deg.
local time 2 = 12:00:11
azimuth 2 = 115.91 deg.
For segment CD we have:
L = 25.0 pixels
H = 432.0 pixels
date = 2014-04-01 (April 1st 2014)
latitude = 8.815315
longitude = -82.425166
time zone = -5
DST = 0 (Daylight Saving Time, there is no DST in Panama)
The results obtained by means of method 1 (here is a description of method 1):
elevation = 86.69 deg. (cell B55 in the spreadsheet)
cosH = 1.00092
cosH corrected = 1.00000
local time 1 = 12:33:30
azimuth 1 = 180.0 deg.
local time 2 = 12:33:30
azimuth 2 = 180.0 deg.
In the case of segment CD we have an ugly thing when the value cosH is greater than 1. In this case it's impossible to determine the hour angle so we must limit cosH to 1. That's why corrected cosH was introduced. This is a technical remark. See the detailed description of calculations in method 1 here.
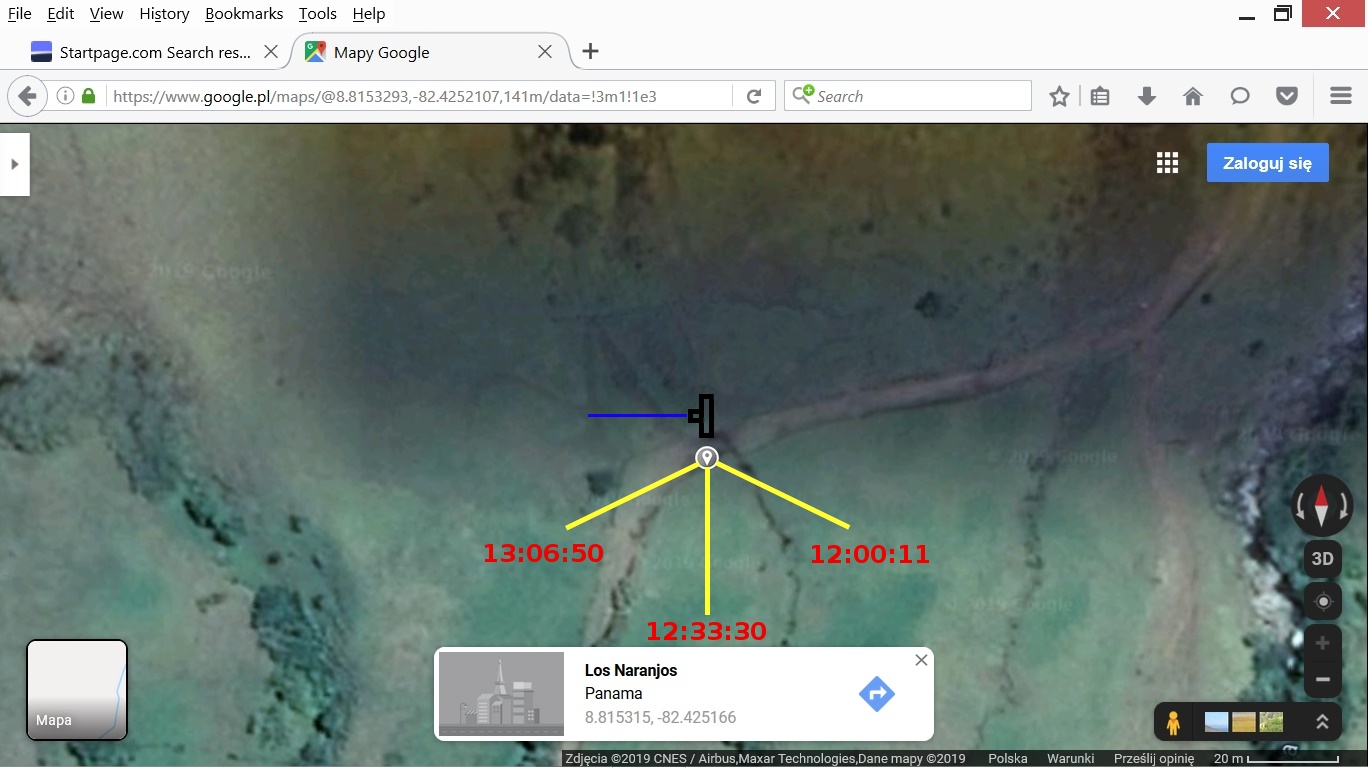
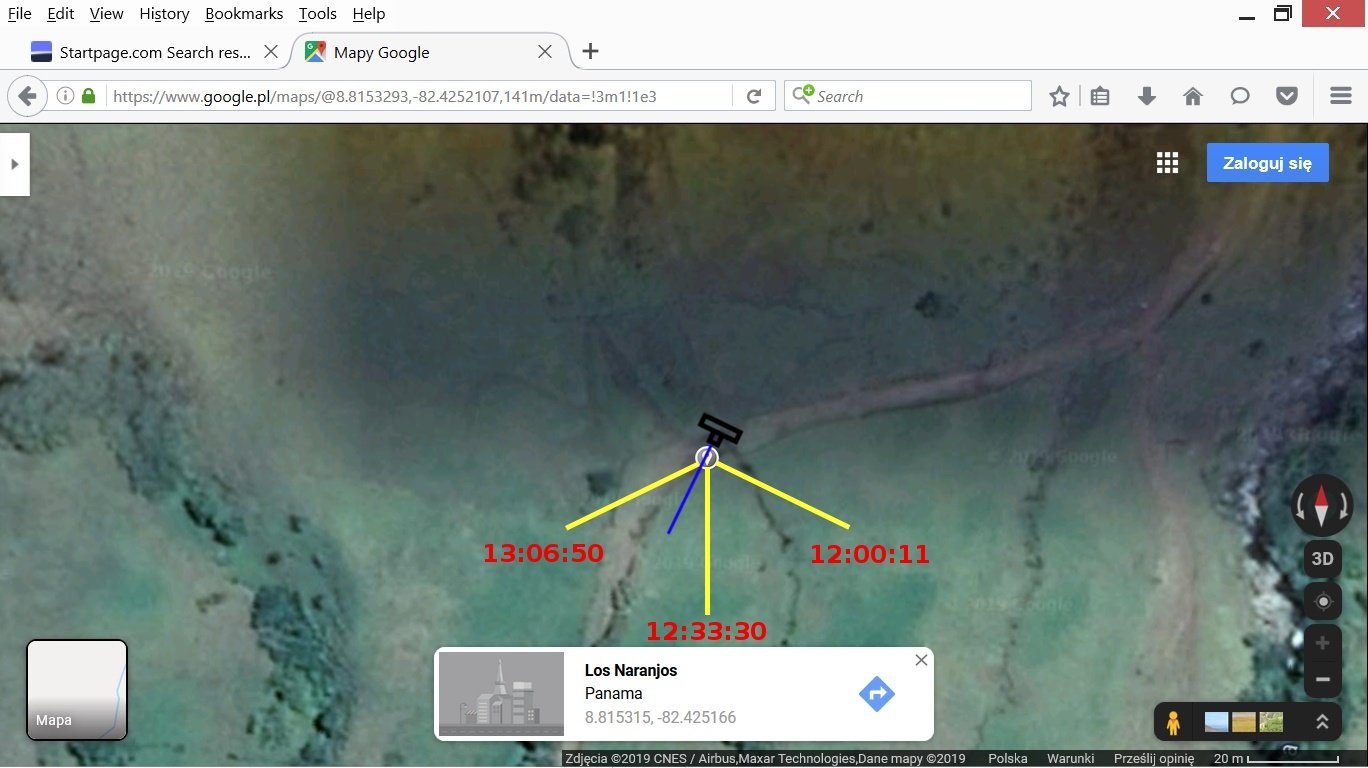
For those two segments we obtained 3 different times and 3 azimuths. Now we must analyse the geometry of the scene in photo 1 to choose the time that fits best.
Version 1: the camera is directed to the west. The blue line indicates the optical axis. That is the line that comes straight out of the camera. The yellow lines indicate our 3 azimuths. From what we see in photo 1 the sun shines from the left side and towards the camera. So in this version the only azimuth that fits that direction is the azimuth for 13:06:50.
Photo 1-3
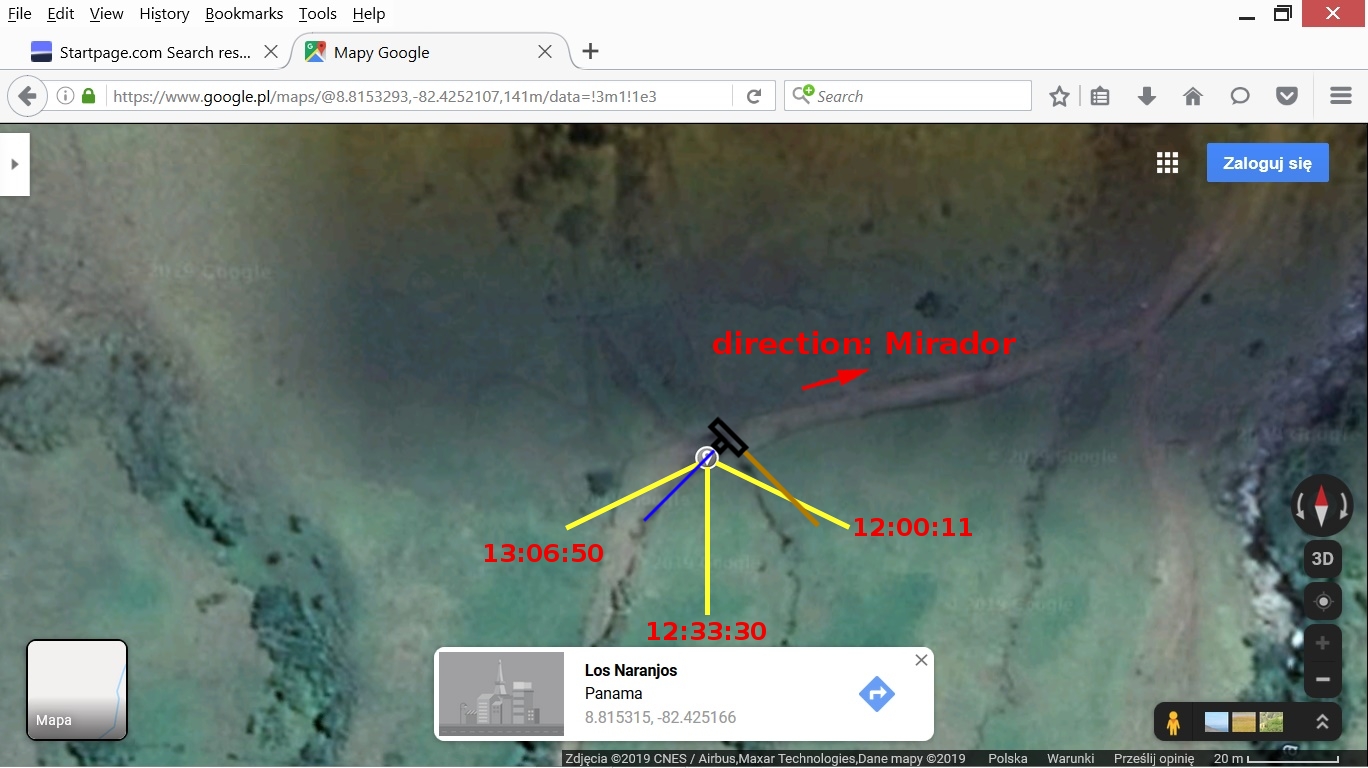
Version 2: the camera is rotated 45 degrees anticlockwise relative to version 1. The azimuth that fits best the scene in photo 1 is the azimuth for 12:33:30. That is the version which I would choose.
Photo 1-4
Here you can find a photo that justify my choice. That is a very similar view of the mountain. You can see the sloping trees behind the girl on her left side of her head. Compare the sloping trees above Kris's head in photo 1. The optical axis in the photo of the girl is directed along the track, exactly in the opposite direction to the direction indicated by the red arrow in photo 1-4. Actually there may be a difference between the directions in both photos. The azimuth of the track is about 257 degrees. I assumed that the azimuth of the optical axis of the camera in photo 1 is 225 degrees (the difference is 32 degrees).
Let's compare photo 1-4 with the photo below. That is the position of Lisanne in photo 3. (See my analysis of photo 3.)
Photo 1-5
In the case of photo 3 I would choose the time 11:41:39 of taking that photo. Where does the difference come from? The difference is about one hour. Where is the error? That is the same place so it is logical that the times of taking photo 1 and photo 3 should be similar.
Version 3: the camera is rotated 45 + 19.09 = 64.09 degrees anticlockwise relative to version 1. The azimuth that fits best the scene in photo 1 is the azimuth for 12:33:30. The angle of the rotation was chosen in the way so that the optical axis would be perpendicular to the azimuth for 12:00:11.
Photo 1-6
Version 4: the camera is rotated 45 + 19.09 + 5 = 69.09 degrees anticlockwise relative to version 1. We have two azimuths that fit the scene in photo 1: the azimuth for 12:33:30 and the azimuth for 12:00:11.
Photo 1-7
Below I will show some photos justifying my assumption that photo 1 and photo 3 were taken at the same place.
This is a photo from this film (at 0:44). The photo shows the place where photo 3 (Lisanne on the El Pianista trail) was taken.
Photo 1-8
The next photo from that film (at 0:50) probably shows the sloping trees which we see in photo 1 (the trees near the cow; compare the trees above Kris's head in photo 1).
Photo 1-9
The photo below comes from this film (at 1:39). It shows the place where photo 3 was taken.
Photo 1-10
The next photo from that film (at 1:43).
Photo 1-11
The next photo from that film (at 1:46). This photo shows the view which we see in photo 1: a very similar view of the mountain and the sloping trees on the right side of the photo.
Photo 1-12
Look at the photo below.
Photo 1-13
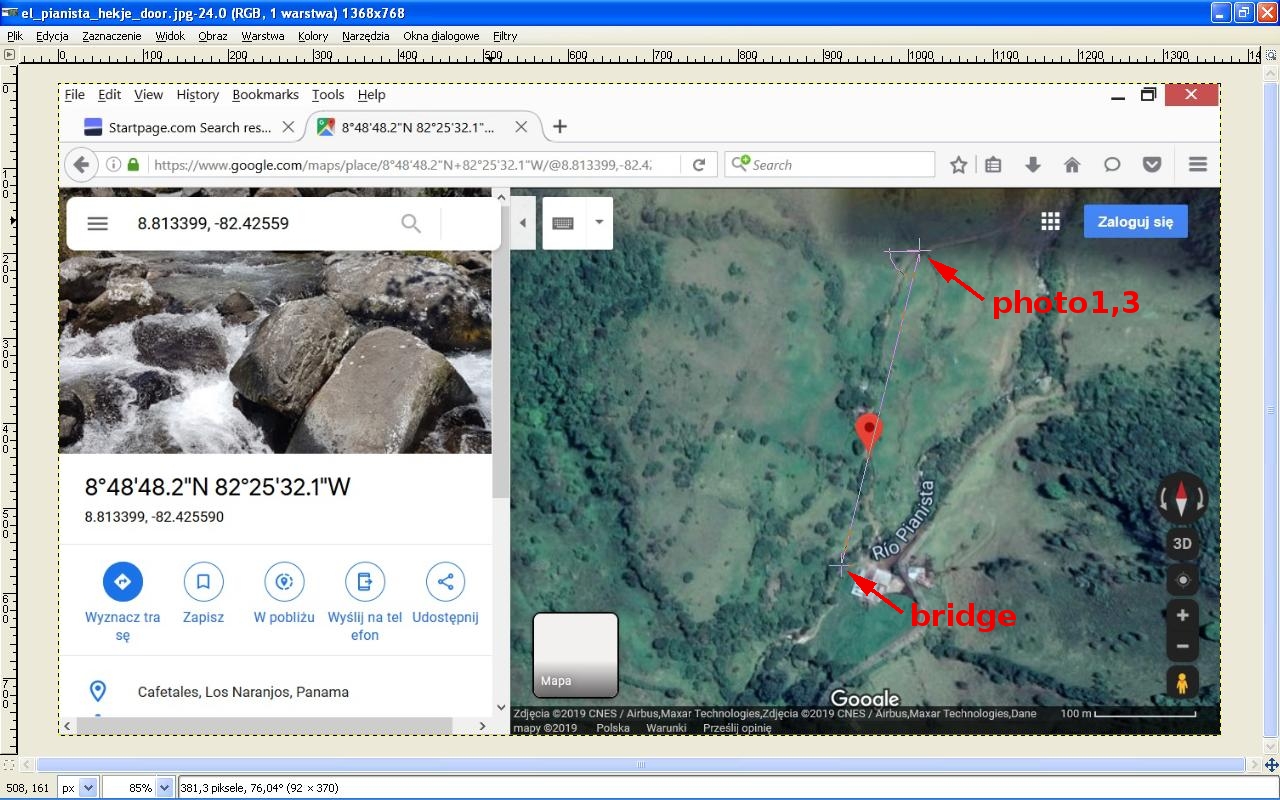
This is a map showing the distance between the bridge in photo 2 and the place in photo 1. The distance is about 320 m in a straight line. It should take no more than 10 minutes to get from the bridge to the place where photo 1 was taken. My earliest approximation of taking photo 2 is 11:08 (See here). So the girls may have reached the place where photo 1 was taken at about 11:18.
From what we see in photo 1-4 the direction of sunlight should be somewhere between the blue line and the brown line which is perpendicular to the blue line. I chose version 2 of the above versions of possible directions.
Here are the times and azimuths corresponding to both lines:
blue line: azimuth = 225 deg., time = 12:49:54
brown line: azimuth = 135 deg., time = 12:17:07
Both the above azimuths determine the range of time of taking photo 1: that is between 12:17:07 and 12:49:54. The girls may have come to the place at about 11:18, but the earliest time of taking photo 1 is 12:17:07, according to my estimation. So the question arises: what were they doing such a long time? That is the problem with this photo. Maybe the girls were at the place between 12:17:07 and 12:49:54, but the day before.
Now look at the photo 4 below. It was taken at the same place as photo 1 and 3. Lisanne is standing almost at the same place as in photo 3. The view in this photo is almost in the opposite direction to the direction in photo 1. Look at the shadows cast by the posts on the right side of the photo. They are directed towards the photographer. The sun in photo 4 shines at the back of Lisanne which is consistent with the shadows cast by the posts. Why does the sun shine at her back in photo 1?
Photo 4.
There are no cast shadows on the ground in photo 1. We do not have a vertical or horizontal line that could be a reference line. The error made in my calculations of the sun's elevation may be significant in the case of photo 1. However I think there is something wrong when you compare the directions of sunlight in photo 1 and photo 4.
Of the photos taken on the El Pianista trail photo 1 was presented first in the Break Free film in April, 2016. It was shown before photo 2. Two things need to be checked: 1) Was photo 1 taken after photo 2? 2) What is the difference between the time of taking photo 1 and other photos taken at the same place (photo 3 and photo 4)?
Below is another version of photo 1. I downloaded it from this photo collection.
Photo 1 (2)
That is probably a better version of photo 1. It is not cut as photo 1 above.
Let's repeat our calculations in the case of photo 1 (2).
Segment AB:
L = 37.0 pixels
H = 232.0 pixels
date = 2014-04-01 (April 1st 2014)
latitude = 8.815315
longitude = -82.425166
time zone = -5
DST = 0 (Daylight Saving Time, there is no DST in Panama)
The results obtained by means of method 1 (here is a description of method 1):
elevation = 80.94 deg. (cell B55 in the spreadsheet)
local time 1 = 13:06:02
azimuth 1 = 243.51 deg.
local time 2 = 12:00:59
azimuth 2 = 116.48 deg.
For segment CD we have:
L = 19.0 pixels
H = 303.0 pixels
date = 2014-04-01 (April 1st 2014)
latitude = 8.815315
longitude = -82.425166
time zone = -5
DST = 0 (Daylight Saving Time, there is no DST in Panama)
The results obtained by means of method 1 (here is a description of method 1):
elevation = 86.41 deg. (cell B55 in the spreadsheet)
cosH = 1.00063
cosH corrected = 1.00000
local time 1 = 12:33:30
azimuth 1 = 180.0 deg.
local time 2 = 12:33:30
azimuth 2 = 180.0 deg.
The new calculations yield similar results. The difference in time is no more than 1 minute. In the case of segment CD the result is the same.
What is interesting is that the file which I downloaded is IMG_0482 (1).JPG. That would mean that the number of photo 1 is 482. The time of taking photo is 11:25:27 (corrected EXIF time).
Here is another photo which I downloaded from the photo collection.
IMG_0485.jpg
The corrected EXIF time of taking the photo is 11:25:36. The view in the photo is the same as in photo 4. According to EXIF time photo 482 and photo 485 were taken at the similar time. However the direction of sunlight indicates that the time is clearly different. The shadows of the posts on the right side of the track are cast along the track in photo 485. The shadow cast by the post on the right side of Lisanne's head is cast approximately perpendicular to the track in photo 482. So we have 2 photos taken approximately at the same time but the directions of sunlight in the photos are incompatible.
Let's calculate what would be the minimal difference in angles.
The position of the sun at 11:25:27 (corrected EXIF time for photo 482):
elevation = 72.61
azimuth = 102.61
The position of the sun at 12:17:07 (the brown line in photo 1-4, see the comment about the brown line above)
elevation = 84.21
azimuth = 135.00
difference = 135.00 - 102.61 = 32.39.
Below is a photo illustrating the difference between the angles:
Photo 1-14
Is it possible to measure such a difference in two different photos? We must remember that this is a conservative estimation (see the comment below photo 1-4 about the azimuth of the optical axis). If we assume that the azimuth of the optical axis is 235, then the difference is 42.39 degrees.
Another argument: look at the shadows cast by the posts on the left in photo 1-10. Then look at the girl and her shadow in photo 1-11. The girl is going with her back turned towards the posts in photo 1-10. You can predict the direction of her shadow. That's what we expect when we compare photo 4 and photo 1.
Maybe taking a test photo exactly in the same direction at 11:25 on April 1st would resolve the problem?
Below is photo 1 illustrating the direction at which the optical axis was directed.
Photo 1 (3)









_center.JPG)