Photo 2 - geometry of a shadow

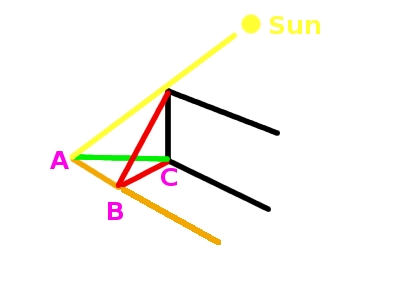
A photo of Kris on the bridge on the El Pianista trail. This is an experimental method. The idea is based on the analysis of the geometry of the shadow in photo 2.

The time of taking photo 2 obtained with this method is 11:08:06.

Below you can see a more abstract picture of the scene in photo 2.

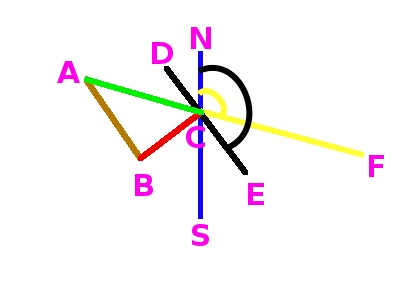
The drawing below shows the geometry of the shadow cast on the bridge by the barrier. It's a view of the bridge from overhead.

the red segment BC - the shadow length measured here (denoted as L)
the green segment AC - the real shadow cast by the point on the barrier
the black segment DE - the barrier
the yellow segment CF - the direction of sunlight
the blue segment NS - the north-south direction

H - the object height (the height of the barrier)

segment BC = L

angle NCF = the sun's azimuth
angle NCE = the azimuth of the barrier (the azimuth of the bridge)

e - sun's elevation

tan(e) = H/AC (1) (see formula (8) in [1])
and
AC = H/tan(e) (2)

triangle ABC - a right triangle

From definition of sine
BC/AC = sin(BAC) (3)

Some relations between angles
BAC = ACD = ECF = NCE - NCF (4)

From (3) and (4) we have
BC/AC = sin(NCE - NCF) (5)
and
BC = AC * sin(NCE - NCF) (6)

From (2) and (6) we have
BC = H/tan(e) * sin(NCE - NCF) (7)

The segment BC was measured (the segment denoted L in photo 2). The value H was measured too. The angle NCE can be measured on the map (the azimuth of the barrier on the bridge, see below). We have to determine such e and NCF that satisfy equation (7). In other words, we have to find sun's elevation and azimuth that satisfy equation (7).

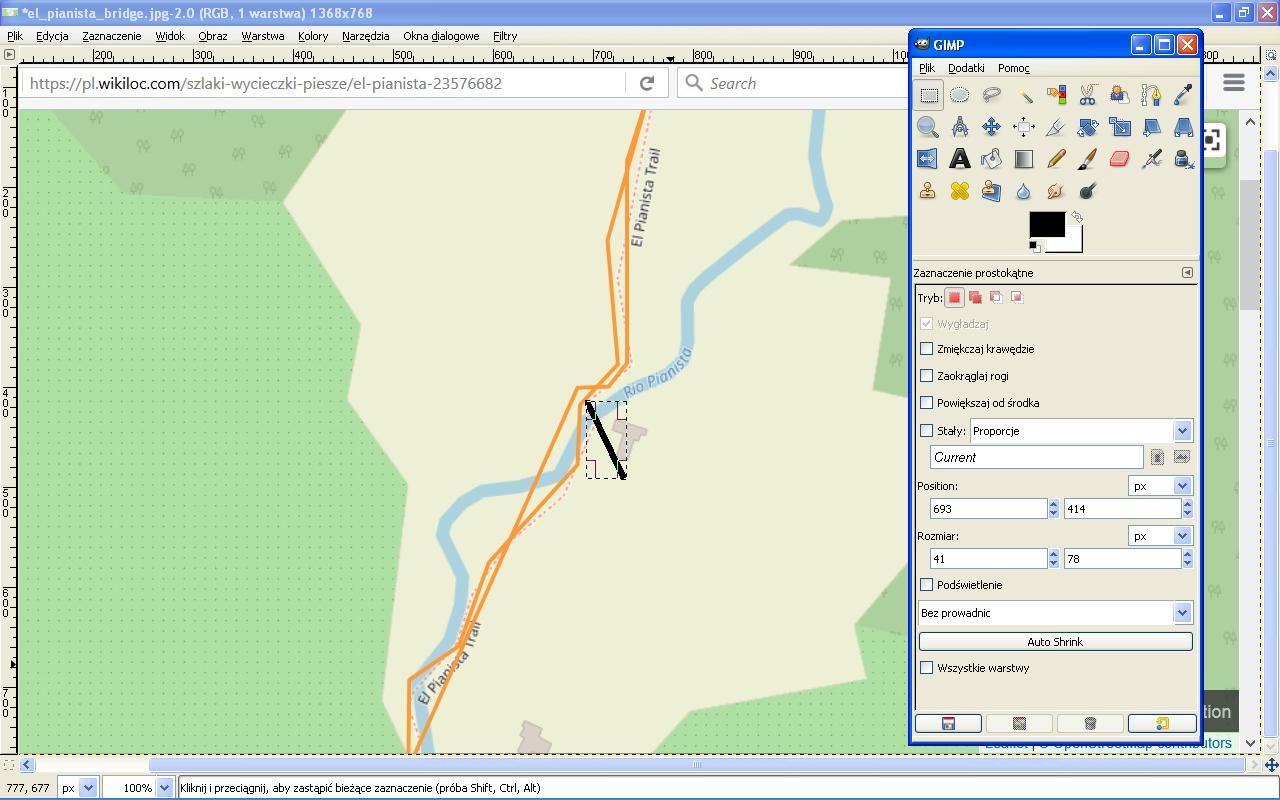
The following map enables us to determine the azimuth of the bridge:

It is a screen cast of the map on this site. I added the black line (segment) so that the azimuth of the bridge would be clearly visible. Using GIMP I measured the lengths of sides of the rectangle determined by the black segment:
X = 41, Y = 78 (in pixels).

The value of the azimuth of the bridge is determined by the following formula:
Azb = 90 + atan(78.0/41.0) = 152.27 deg.

First we need some helper function. Below is an algorithm of the function that calculates the time of a day when sun's azimuth is equal to the given azimuth. The while loop traverses from TimeOfSunrise to TimeOfSunset. The hour in the while loop changes by 1 second. That hour is chosen at which the difference between the given azimuth and the calculated azimuth is the smallest.

double calculateTimeUsingAzimuth(Year, Month, Day, Latitude, Longitude, TimeZone, DST, GivenAzimuth, GregorianCalendar[] Sunriseset)
begin
 TimeOfSunrise = Sunriseset[0]
 TimeOfSunset = Sunriseset[2]
 hours = TimeOfSunrise
 while hours <= TimeOfSunset
 begin
    elevation, azimuth = calculateSunPosition(Date(hours), Latitude, Longitude, TimeZone, DST)
    if difference > abs(azimuth - GivenAzimuth) then
    begin
       difference = abs(azimuth - GivenAzimuth)
       HoursFound = hours
       ElevationFound = elevation
       AzimuthFound = azimuth
    end
    hours = hours + 1 sec
end

Here is an implementation of the above algorithm: the calculateTimeUsingAzimuthSunriseset method in the following class BasicSolarShadow.java. (The whole project.)

Here is an algorithm that determines the time of taking photo 2. The algorithm is based on formula (7). The while loop traverses from the time of sunrise to HoursForAzimuth. The hour in the loop is inreased by 1 second. In each pass of the loop sun's elevation and azimuth are calculated and then the length of the shadow (formula (7)). That hour is chosen at which the difference between the given shadow length and the calculated shadow length is the smallest.

BC - the measured shadow length

// Calculate the time of sunrise, solar noon (transit), sunset
// SPA algorithm is used (implemented in Java by Klaus Brunner)
GregorianCalendar[] SunriseTransitSet = calculateSunriseTransitSet(Date, Latitude, Longitude, DeltaT)
// Calculate the hour when sun's azimuth is equal to the azimuth of the barrier
// The helper function described above is used
HoursForAzimuth = calculateTimeUsingAzimuthSunriseset(Year, Month, Day, Latitude, Longitude, TimeZone, DST, Azb, SunriseTransitSet)
TimeOfSunrise = SunriseTransitSet[0]
hours = HoursForAzimuth
while hours >= TimeOfSunrise
begin
   elevation, azimuth = calculateSunPosition(Date(hours), Latitude, Longitude, TimeZone, DST)
   slength = H/tan(elevation) * sin(Azb - azimuth)

   if difference > abs(slength - BC) then
   begin
      difference = abs(slength - BC)
      HoursFound = hours
      ShadowLenFound = slength
      ElevationFound = elevation
      AzimuthFound = azimuth
   end
   hours = hours + 1 sec
end

An implementation of the above algorithm: BarrierShadowGeometry.java. (The whole project.)

Results obtained in case of photo 2:
HoursFound -> time = 11:08:06
ShadowLenFound=51.0049
AzimuthFound =99.61 deg.
AC=64.15 // from formula (6)
ElevationFound=68.4 deg.

The time of taking photo 2 with this method is 11:08:06.

References

[1] Frode Eika Sandnes "Determining the Geographical Location of Image Scenes based on Object Shadow Lengths"
https://www.researchgate.net/publication/220541439_Determining_the_Geographical_Location_of_Image_Scenes_based_on_Object_Shadow_Lengths
accessed 28.06.2019.

[2] Kevin Karney "Basic Solar Positional Astronomy"
http://www.precisedirections.co.uk/Sundials/Basic%20Solar%20Positional%20Astronomy.pdf
accessed 28.08.2019.

[3] Simon Wheaton-Smith "Illustrating Time’s Shadow"
http://www.illustratingshadows.com/mainBook.pdf
accessed 4.09.2019

[4] Abhik Milan Pal, Subhra Das "Analytical Model for Determining the Sun’s Position at All Time Zones"
http://article.sapub.org/10.5923.j.ijee.20150503.03.html
accessed 29.10.2019.

[5] Ibrahim Reda, Afshin Andreas "Solar Position Algorithm for Solar Radiation Applications"
https://www.nrel.gov/docs/fy08osti/34302.pdf
accessed 29.10.2019