Photo 2 (476)

A photo of Kris on the bridge on the El Pianista trail.

Photo 2-1

A fragment of the above photo is below. You can see clearly the shadow cast by the barrier on the bridge. I will use the shadow to determine the time of taking photo 2. The method of determining the time of taking a photo is described here.

Photo 2-2

Here are the data needed to calculate the time of taking photo 2:
L = 51.0 pixels (shadow length, look at the red letter L in the first photo above)
H = 162.0 pixels (object height, look at the red letter H in the first photo above)
date = 2014-04-01 (April 1st 2014)
latitude = 8.812407
longitude = -82.425896
time zone = -5
DST = 0 (Daylight Saving Time, there is no DST in Panama)

Results obtained by means of method 1:
elevation = 72.53 deg (cell B55 in the spreadsheet)
local time 1 = 13:41:56
azimuth 1 = 257.51 deg.
local time 2 = 11:25:05
azimuth 2 = 102.49 deg.

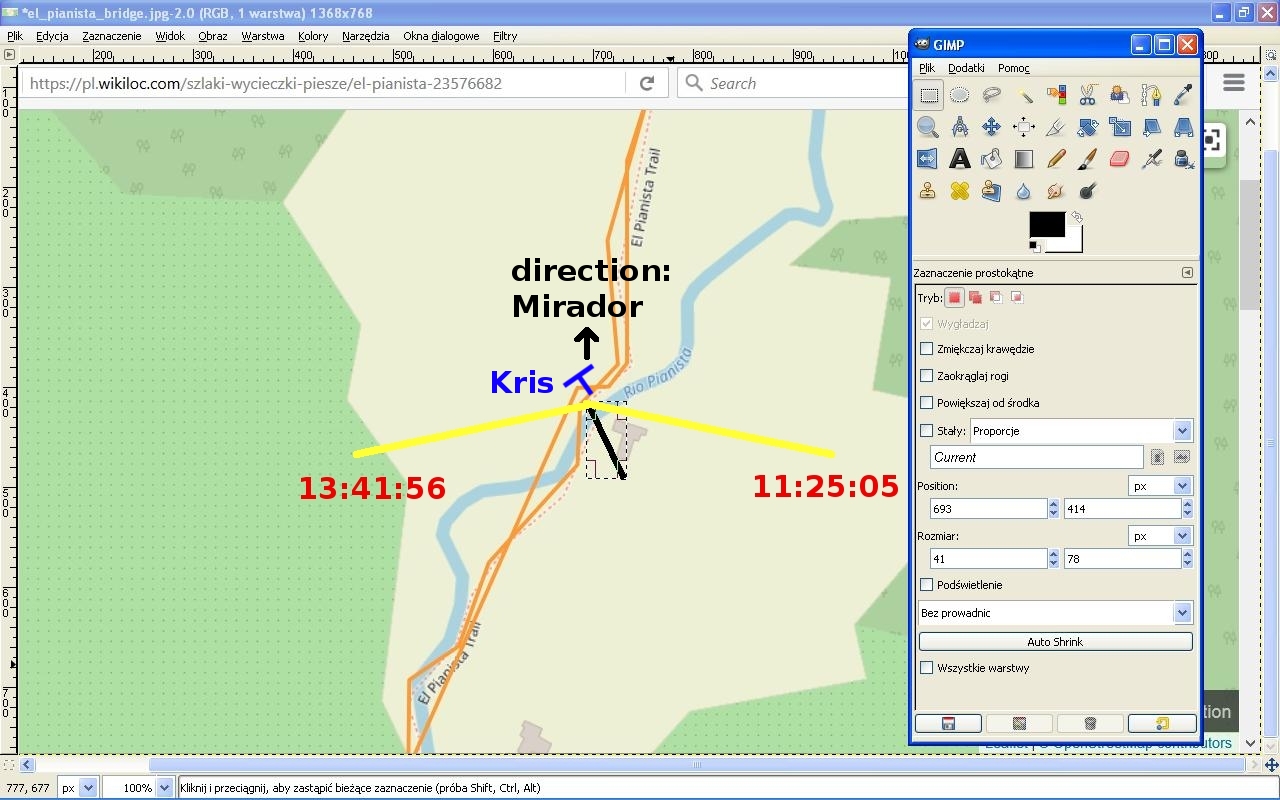
We obtained two times and two associated azimuths. Elevation is the same in both cases. The difference is in azimuths, so we must analyse the directions in photo 2. Below is a photo showing the directions determined by the resulted azimuths.

Photo 2-3

The photo was obtained from a screen cast of the map of the El Pianista trail on this site. The black line shows the direction of the bridge. This is only approximation of the direction of the bridge. The yellow lines show the directions of sunlight determined by the above azimuths. The blue rotated letter T symbolizes Kris's body on the bridge. I assumed that her back is directed to the north-west. In photo 2 we see that the sun shines from Kris's left side, so from my assumption about the direction of Kris's body appears that the direction of sunlight indicates the time 11:25:05 of taking photo 2.

If we want to be precise, we must take geometry of the shadow on the bridge into consideration. It was done here. That is another method to determine the time of taking a photo and it can be more precise in this case. The result obtained by means of that method is 11:08:06.

We have two model approximations of the time of taking photo 2. The simplest way to test the approximations is to go to the bridge during sunny weather on April 1st and take a test photo.

Below is a photo combination showing what position of the cast shadow we should expect on the bridge.

Photo 2-4

The shadow of the barrier is cast on the second element on the bridge on the right (the second row along the bridge on the right).

Another photo of the bridge is below. Look at the last sloping rail of the barrier on the right on the other side of the bridge. That sloping rail determines the shape of the shadow behind Kris.

Photo 2-5

And another photo of the bridge. It is a side view of the bridge. The sloping rail is clearly visible.

Photo 2-6

A Blender model of the iron bridge

With what accuracy can the time of taking photo 2 be determined by means of taking a test photo?

Here is a photo that can give an answer to the question:

Photo 2-7

The above photo combination was made of photos obtained by rendering the Blender model several times. The time was set at five-minute intervals. The model needs the photo of texture in the directory where the Blender file is located. I used Blender version 2.79b and the add-on that properly sets the position of the Sun at a given time. Photo 2-7 shows that 11:13 is a best match for the time of taking photo 2 (compare to photo 2-2). It also shows that it is possible to determine the time of taking photo 2 with an accuracy of 5 minutes.

The use of the Blender model is a relatively independent method for determining the time of taking photo 2.

How were the dimensions of the bridge determined? I assumed that the height of Kris is 167 cm (following the wikipedia website), and I used photo 2 to determine the height of the barrier of the bridge and the width of the bridge.

These are the calculations and links to photos with measured dimensions:

Kris' height 423 pixels

the height of the barrier without the railing 243 pixels
barrier_height / 243 = Kris_height / 423
barrier_height = 167 cm * 243 / 423 = 95.94 cm -> 96 cm

the width of the bridge 309 pixels
bridge_width / 309 = Kris_height / 423
bridge_width = 167 cm * 309 / 423 = 121.99 cm

And the following calculations for the height of the barrier with the railing:

the height of the barrier without the railing 70 pixels

the height of the barrier with the railing 74 pixels
barrier_height1 / 74 = barrier_height / 70
barrier_height1 = 96 cm * 74 / 70 = 101.5 cm