Determining the time of taking a photograph
by measuring shadow lengths in the photograph
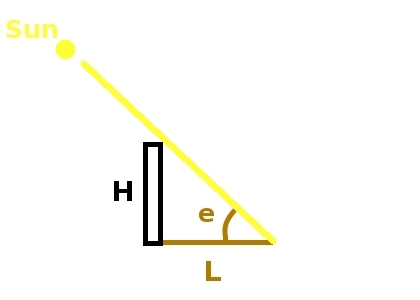
The idea comes from this work [1]. The drawing below illustrates the relationship between the sun elevation, the object height and the shadow length.
The formula
e = atan(H/L) (1)
is used to determine the sun's elevation.
e - the sun's elevation,
H - an object's height, L - the length of the shadow.
atan is the inverse of the tangent function.
Knowing the sun's elevation, we can determine the time of the day when a photo was taken.
The following methods can be used to determine the time of taking a photo:
Method 1
The method uses a modified spreadsheet downloaded from this website.
These are two versions of the spreadsheet:
NOAA_Solar_Calculations_day_shadow.ods OpenOffice.org Calc
NOAA_Solar_Calculations_day_shadow.ods MS Excel
The modified spreadsheet calculates the time of taking a photo when input data are set properly.
How to use the spreadsheet?
1. Measure the height of an object in the photograph. Measure the shadow cast by the object. The measured values can be in pixels, centimeters, inches or millimeters. Both values (the object's height and the shadow length) must be in the same unit.
Here is an example of a photo where an object height H and the length of the cast shadow L are denoted.
2. Open the spreadsheet. Set latitude, longitude of the place in the photo.
Set the time zone. Remember to add 1 to the number of time zone if DST is in effect.
DST means Daylight Saving Time (called summer time as well).
Set the date. Set the height (cell B49 in the spreadsheet) measured in point 1.
Set the measured shadow length (cell B50 in the spreadsheet).
The cells C73 and C75 will show the calculated times of taking the photo.
Now you have 2 times of the day for the input data. How to choose between the two times? One of the method is to analyse direction of the cast shadow in the photograph. The example of such an analysis is here.
3. The sun declination and EOT (Equation of Time) are taken for the time 12:00. If you want to use those parameters for a different time, you must change the content of cell B51 (by default set to =T121) and B52 (by default set to =T121). For example, if you want to use declination and EOT for 10:00, you must set cell B51 to =T101 and cell B52 to =V101.
A detailed description of my modifications of the NOAA spreadsheet is here.
Method 2
A minimum of mathematical formulas. The rest of mathematics is hidden on the NOAA Solar Calculator website and the sunearthtools website.
1. Measure the height of an object in the photograph. Measure the shadow cast by the object. The measured values can be in pixels, centimeters, inches or millimeters. Both values (the object's height and the shadow length) must be in the same unit.
2. Go to the sunearthtools website.
3. Insert proper geographic coordinates of the place in the examined photograph (latitude, longitude).
Set the proper date. Set the time zone. Check or uncheck DST.
DST means Daylight Saving Time (called summer time as well).
Click the Execute button.
For example in our demonstration photo
latitude=8.812407 longitude=-82.425636
Time Zone=-5
date=2014.04.01. (April 1st 2014)
Our example relates to Panama. There is no DST in Panama.
The place you have in the photograph should be displayed on the map on the website.
Under the map there is a table of the sun's elevations and azimuths for the given day. You will need the table with 5 minutes accuracy.
Set step to 5 minutes in the field above the table. Click the execute button above the table (not the one above the map).
Now you have the table of the sun's elevations and azimuths for the given day with 5 minutes accuracy. You can print the table or save it to a pdf file. (see el_pianista_photo1_2014_04_01_12_00.pdf; the table is on pages 3-5)
4. Open the spreadsheet Shadow.xls.
The spreadsheet contains four cells. Cell B1 (an object's height) and B2 (the length of the shadow) are input values. Cell B3 (the sun's elevation) is based on formula (1) (see above). Cell B4 converts the sun's elevation from radians to degrees.
Insert measured values in the proper fields of the spreadsheet.
For example height=162, shadow length=51
Click on cell B3. Now cell B4 should display the measured sun's elevation in degrees. In our example cell B4 should display the value 72.525226.
5. Check in the table from sunearthtools (point 2) what time corresponds to the elevation determined in point 4.
In our example there are two ranges of time
11:25 - 11:30 (elevations 72.49 - 73.7)
13:40 - 13:45 (elevations 71.8 - 73)
6. Go to the NOAA Solar Calculator.
Insert geographic coordinates of the place (latitude, longitude), time zone. Check or uncheck DST. Set the proper date.
7. Set the time so that the elevation in results will display the value 72.53.
(The elevation is the right field under the Az/El label on the right side of results).
From point 5 you know that the time is between 11:25 and 11:30 (the first range).
Set properly hours, minutes and seconds to obtain the value 72.53 in the elevation field. This is a method by trial and error, but the hour is known. For minutes there are maximum 5-6 values to set. A little more work should be with seconds.
In this way you can determine that the first time is 11:25:05.
Using the second range of time (13:40 - 13:45) you can determine the second time. In our example it is 13:41:56.
Remember that every time you change the time (the hour, minute, second) you should click another field on the website so that the changed time will be reflected in results. There is no execute button on this website as on the sunearthtools website.
Now you have 2 times of the day when the elevation was 72.53.
How to choose between the two times? One of the method is to analyse direction of the cast shadow in the photograph. The example of such an analysis is here.
Method 3
A computer program that computes the time of taking a photograph from lengths of shadows.
BasicSolarShadow.java
BasicSolarCalculator.java
(the whole project)
The program is based on the calculations described in [2]. The program gives very similar results to the results obtained by means of method 1.
References
[1] Frode Eika Sandnes "Determining the Geographical Location of Image Scenes based on Object Shadow Lengths"
https://www.researchgate.net/publication/220541439_Determining_the_Geographical_Location_of_Image_Scenes_based_on_Object_Shadow_Lengths
accessed 28.06.2019.
[2] Kevin Karney "Basic Solar Positional Astronomy"
http://www.precisedirections.co.uk/Sundials/Basic%20Solar%20Positional%20Astronomy.pdf
accessed 28.08.2019.
[3] Simon Wheaton-Smith "Illustrating Time’s Shadow"
http://www.illustratingshadows.com/mainBook.pdf
accessed 4.09.2019