Angles at the Mirador

These are my estimations of some azimuths of directions visible in photos at the Mirador. The idea is to measure the azimuth of the summit visible in photos at the Mirador and determine the horizontal angle of view of Canon PowerShot SX270 HS. See the appendix in this paper how to calculate the angle of view of a camera.

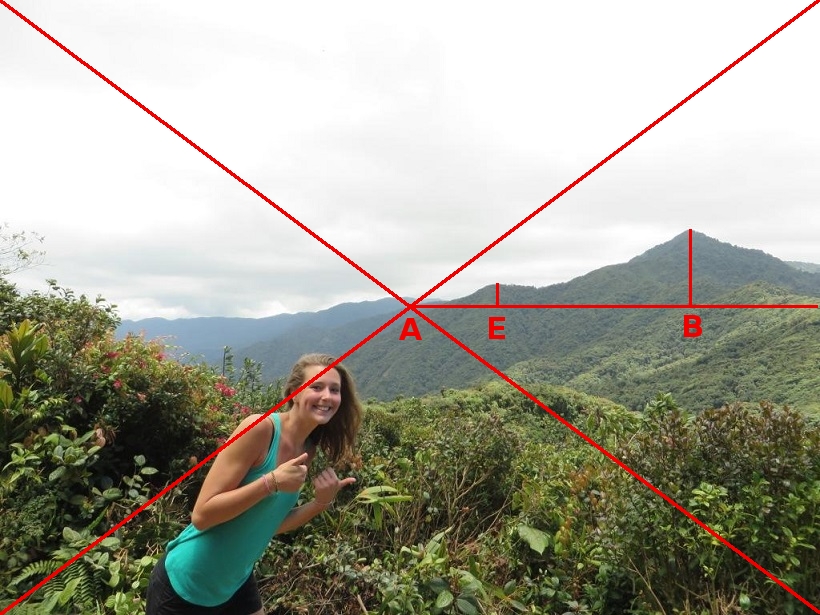
Photo M-1 (photo 500 updated)

point A - azimuth 81.69 (the center of photo 500)
point E - azimuth 90 (East)
point B - azimuth 106.79 (the summit)

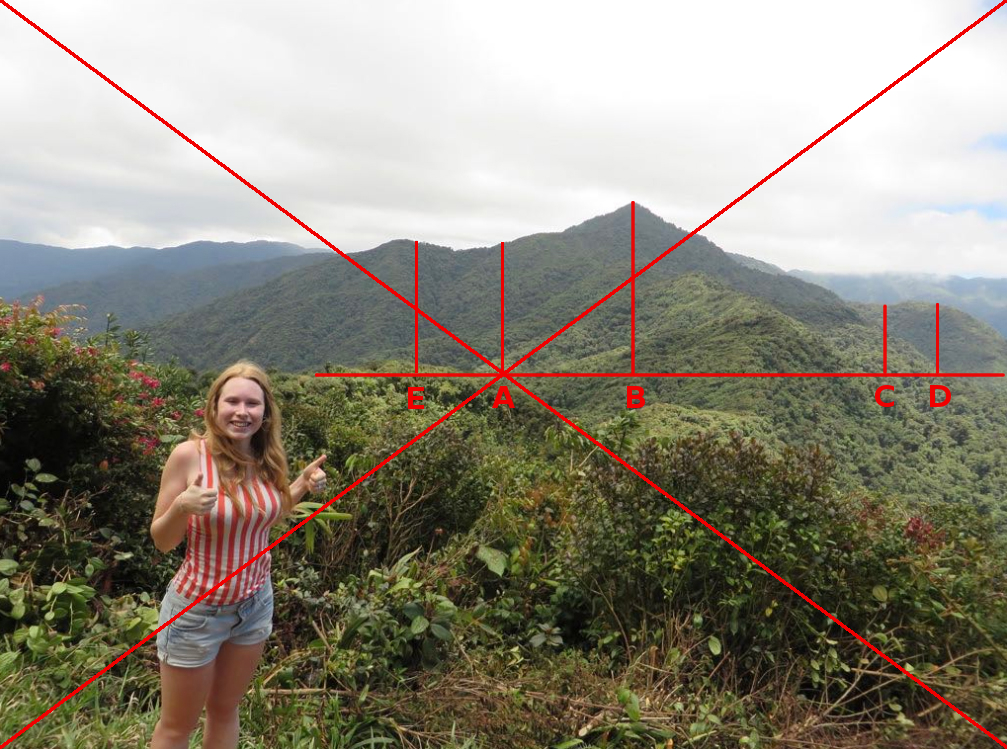
Photo M-2 (photo 501 updated)

point A - azimuth 96.74 deg. (the center of photo 501)
point E - azimuth 90 deg. (East)
point B - azimuth 106.79 deg. (the summit)
point C - azimuth 124.26 deg. (the center of photo 10)
point D - azimuth 127.36 deg. (the left side of photo 499)

Photo M-3 (photo 499 updated)

the azimuth of the center 161.81 deg (photo 499)

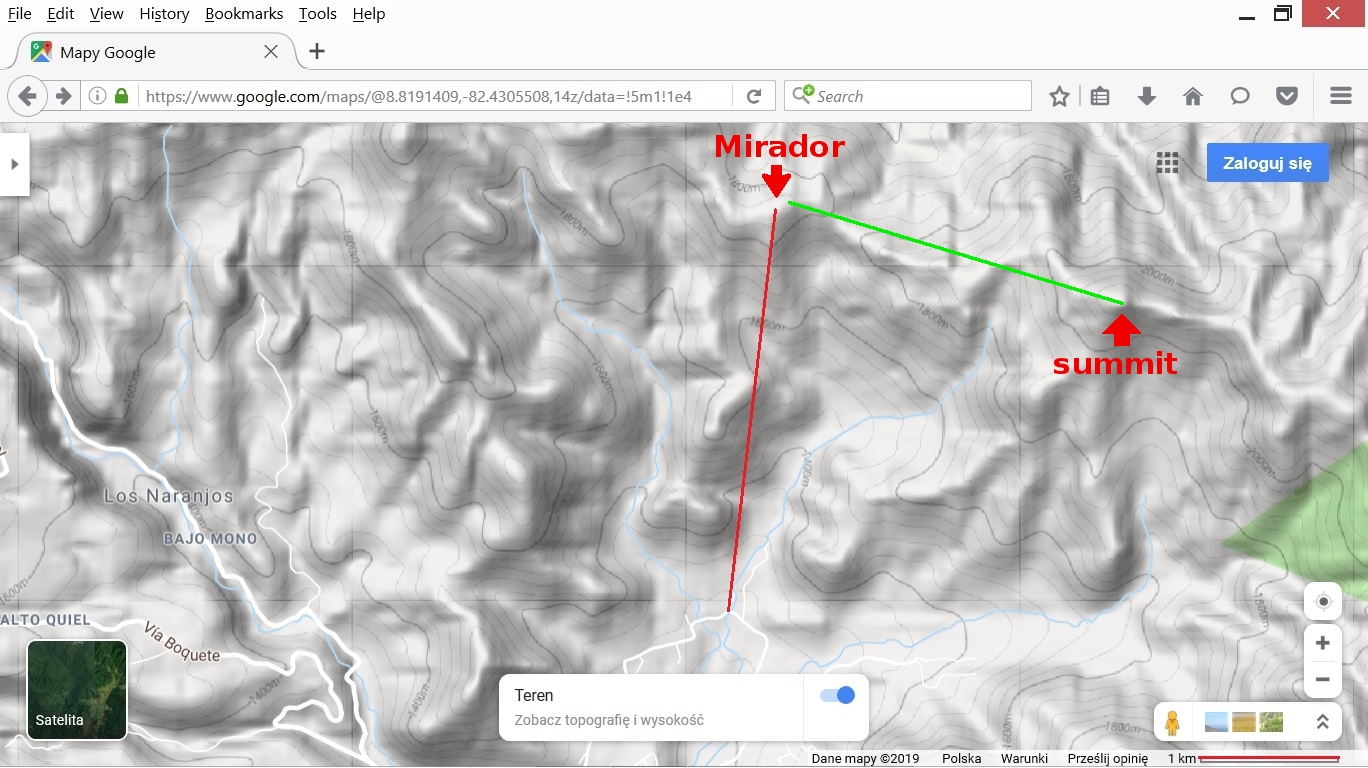
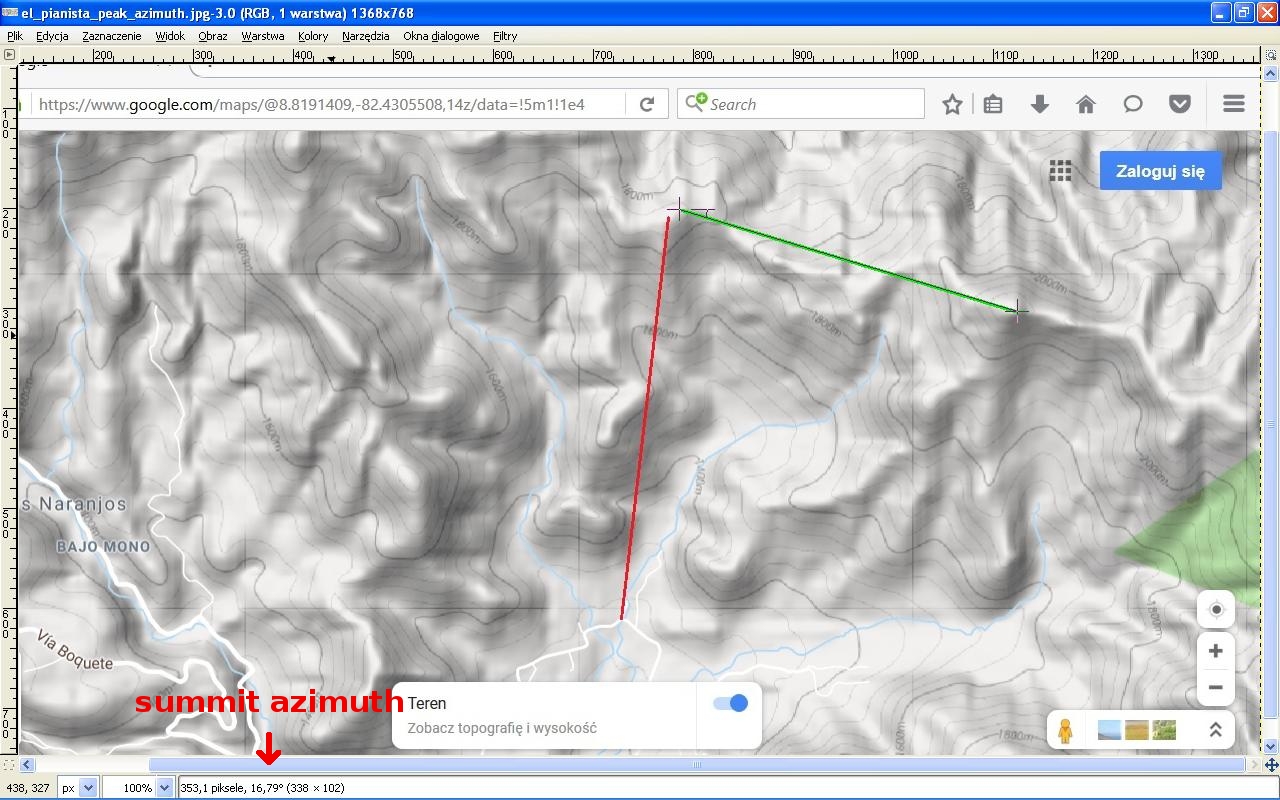
The azimuth of the summit visible in photos at the Mirador

Photo M-4

Photo M-5

The azimuth of the summit = 90 + 16.79 deg. = 106.79 deg.

The horizontal angle of view of Canon PowerShot SX270 HS

The horizontal size of the sensor of the camera h = 6.17 mm
The focal length f = 4.5 mm
The horizontal angle of view = 2 * atan ( h/(2*f) ) = 2 * atan ( 6.17/(2 * 4.5) ) = 68.85 deg.

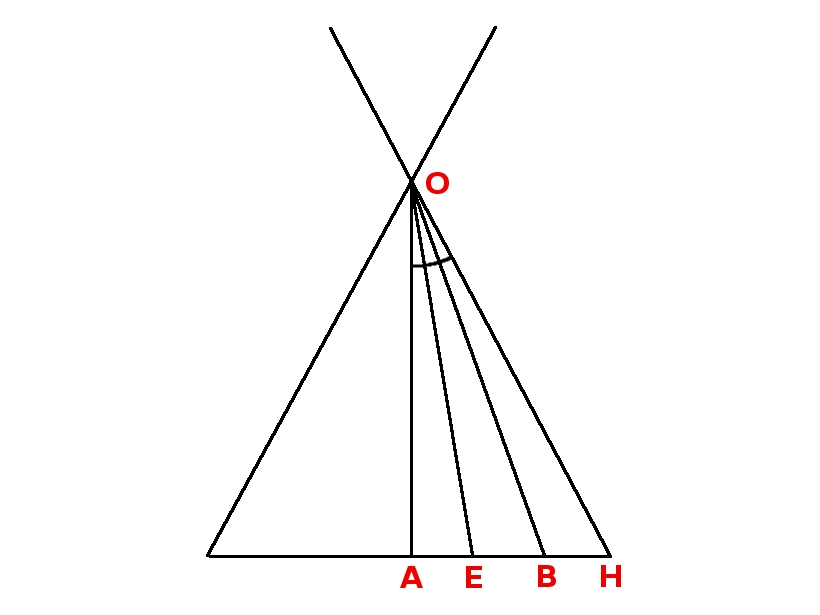
Calculations of azimuths in photo 500

Photo M-6

AOH = 68.89 / 2 = 34.45 deg. (half the horizontal angle of view of the camera)
AB = 280 pixels
AH = 410 pixels
AOB denotes angle AOB
AB / OA = tan(AOB)
AH / OA = tan(AOH) = tan(34.45)
OA = AH / tan(34.45)
tan(AOB) = AB / AH * tan(34.45)
AOB = atan( 280/410 * tan(34.45) ) = 25.10 deg.

AOE = AOB - EOB = 25.1 - 16.79 = 8.31 deg.
the azimuth of the center of photo 500 = 90 - 8.31 = 81.69

We must know where to place point E.
AE / OA = tan(AOE)
AH / OA = tan(AOH) = tan(34.45)
OA = AH / tan(34.45)
AE = AH / tan(34.45) * tan(AOE) = 87 pixels

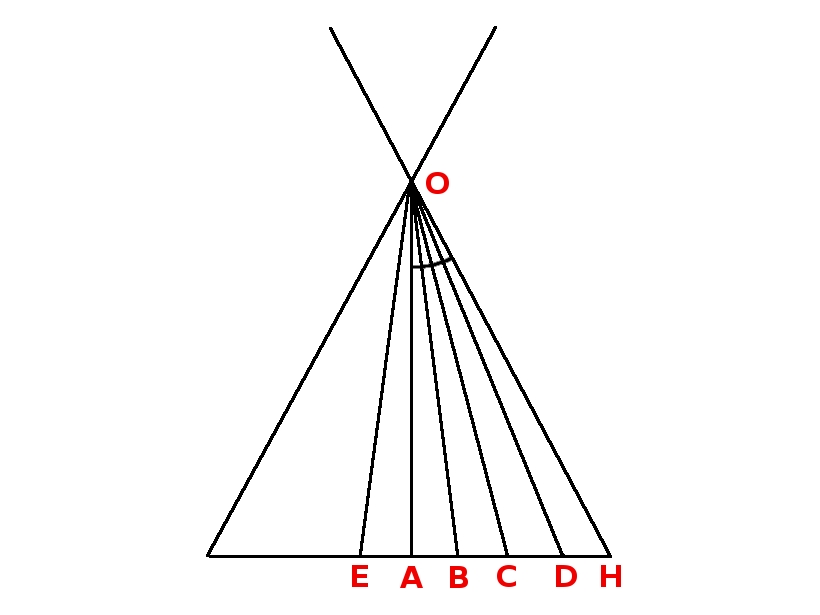
Calculations of azimuths in photo 501

Photo M-7

AOH = 68.89 / 2 = 34.45 deg. (half the horizontal angle of view of the camera)
AH = 503 pixels
AB = 130 pixels
AOB denotes angle AOB
AH / AO = tan(AOH)
AO = AH / tan(AOH)
AB / AO = tan(AOB)
AB = AO * tan(AOB)
AB = AH / tan(AOH) * tan(AOB)
tan(AOB) = AB / AH * tan(AOH)
AOB = atan(130 / 503 * tan(34.45)) = 10.05 deg.

EOA = EOB - EOA = 16.79 - 10.05 = 6.74 deg.
the azimuth of the center of photo 501 = 90 + 6.74 = 96.74 deg.

We must know where to place point E.
AE / AO = tan(EOA)
AO = AH / tan(AOH)
AE = AH / tan(AOH) * tan(EOA) = 503 / tan(34.45) * tan(6.74) = 87 pixels

AC = 382 pixels
AC / AO = tan(AOC)
AO = AH / tan(AOH)
AC = AH / tan(AOH) * tan(AOC)
tan(AOC) = AC/AH * tan(AOH)
AOC = atan(AC/AH * tan(AOH)) = atan(382/503 * tan(34.45)) = 27.52 deg.
the azimuth of the center of photo 10 = the azimuth of the center of photo 501 + AOC =
96.74 + 27.52 = 124.26 deg.

AD = 434 pixels
AD / AO = tan(AOD)
AO = AH / tan(AOH)
AD = AH / tan(AOH) * tan(AOD)
tan(AOD) = AD/AH * tan(AOH)
AOD = atan(AD/AH * tan(AOH)) = atan(434/503 * tan(34.45)) = 30.62 deg.
the azimuth of the left side of photo 499 = the azimuth of the center of photo 501 + AOD =
96.74 + 30.62 = 127.36 deg.

Calculations of azimuths in photo 499

the azimuth of the center of photo 499 = the azimuth of the left side of photo 499 + 34.45 =
127.36 + 34.45 = 161.81 deg.